Things are not what they seem
Many business decisions come down to common sense or relatively simple math. But applying common sense to conditional probability problems can lead to very wrong results as we'll see. As data science becomes more and more important for business, decisions involving conditional probability will arise more often. In this blog post, I'm going to talk through some counter-intuitive conditional probability examples and where I can, I'll tell you how they arise in a business context.
Testing for diseases
This is the problem with the clearest links to business. I'll explain the classical form of the problem and show you how it can come up in a business context.
Imagine there's some disease affecting a small fraction of the population, say 1%. A university develops a great test for the disease:
- If you have the disease, the test will give you a positive result 99% of the time.
- If you don't have the disease, the test will give you a negative result 99% of the time.
You take the test and it comes back positive. What's the probability you have the disease?
The answer is 50%.
If you want an explanation of the 50% number, read the section "The math", if you want to know how it comes up in business, skip to the section "How it comes up in business".
The math
What's driving the result is the low prevalence of the disease (1%). 99% of the people who take the test will be uninfected and it's this that pushes down the probability of having the disease if you test positive.
There are at least two ways of analyzing this problem, one is using a tree diagram and one is using Bayes' Theorem. In a previous blog post, I went through the math in detail, so I'll just summarize the simpler explanation using a tree diagram. To make it easier to understand, I'll assume a population of 10,000.
Of the 10,000 people, 100 have the disease, and 9,900 do not. Of the 100, 99 will test positive for the disease. Of the 9,900, 99 will test positive for the disease. In total 99 + 99 will test positive, of which only 99 will have the disease. So 50% of those who test positive will have the disease.
How it comes up in business
Instead of disease tests, let's think of websites and algorithms. Imagine you're the CEO of a web-based business. 1% of the visitors to your website become customers. You want to identify who'll become a customer, so you task your data science team with developing an algorithm based on users' web behavior. You tell them the test is to distinguish customers from non-customers.
They come back with a complex test for customers that's 99% true for existing customers and 99% false for non-customers. Do you have a test that can predict who will become a customer and who won't?
This is the same problem as before, if the test is positive for a user, there's only a 50% chance they'll become a customer.
How many daughters?
This is a classic problem and shows the importance of describing a problem exactly. Exactly, in this case, means using very very precise English.
Here's the problem in its original form from Martin Gardner:
- Mr. Jones has two children. The older child is a girl. What is the probability that both children are girls?
- Mr. Smith has two children. At least one of them is a boy. What is the probability that both children are boys?
The solution to the first problem is simple. Assuming boys or girls are equally likely, then it's 50%.
The second problem isn't simple and has generated a great deal of debate, even 60 years after Martin Gardner published the puzzle. Depending on how you read the question, the answer is either 50% or 33%. Here's Khovanova's explanation:
"(i) Pick all the families with two children, one of which is a boy. If Mr. Smith is chosen randomly from this list, then the answer is 1/3.
(ii) Pick a random family with two children; suppose the father is Mr. Smith. Then if the family has two boys, Mr. Smith says, “At least one of them is a boy.” If he has two girls, he says, “At least one of them is a girl.” If he has a boy and a girl he flips a coin to say one or another of those two sentences. In this case, the probability that both children are the same sex is 1/2."
In fact, there are several other possible interpretations.
What does this mean for business? Some things that sound simple aren't and differences in the precise way a problem is formulated can give wildly different answers.
Airline seating
Here's the problem stated from an MIT handout:
"There are 100 passengers about to board a plane with 100 seats. Each passenger is assigned a distinct seat on the plane. The first passenger who boards has forgotten his seat number and sits in a randomly selected seat on the plane. Each passenger who boards after him either sits in his or her assigned seat if it is empty or sits in a randomly selected seat from the unoccupied seats. What is the probability that the last passenger to board the plane sits in her assigned seat?"
You can imagine a lot of seat confusion, so it seems natural to assume that the probability of the final passenger sitting in her assigned seat is tiny.
Actually, the probability of her sitting in her assigned seat is 50%.
StackOverflow has a long discussion on the solution to the problem that I won't repeat here.
What does this mean for business? It's yet another example of our intuition letting us down.
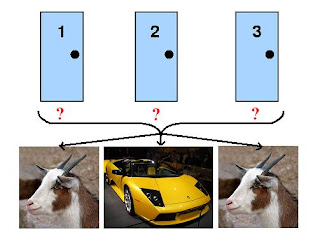
The Monty Hall problem
This is the most famous of all conditional probability problems and I've written about it before. Here's the problem as posed by Vos Savant:
"A quiz show host shows a contestant three doors. Behind two of them is a goat and behind one of them is a car. The goal is to win the car.
The host asked the contestant to choose a door, but not open it.
Once the contestant has chosen a door, the host opens one of the other doors and shows the contestant a goat. The contestant now knows that there’s a goat behind that door, but he or she doesn’t know which of the other two doors the car’s behind.
Here’s the key question: the host asks the contestant "do you want to change doors?".
Once the contestant decided whether to switch or not, the host opens the contestant's chosen door and the contestant wins the car or a goat.
Should the contestant change doors when asked by the host? Why?"
Here are the results.
- If the contestant sticks with their initial choice, they have a ⅓ chance of winning.
- If the contestant changes doors, they have a ⅔ chance of winning.
Once again, this shows how counter-intuitive probability questions can be.
What should your takeaway be, what can you do?
Probability is a complex area and common sense can lead you wildly astray. Even problems that sound simple can be very hard. Things are made worse by ambiguity; what seems a reasonable problem description in English might actually be open to several possible interpretations which give very different answers.
(Sound judgment is needed when dealing with probability. You need to think like a judge, but you don't have to dress like one. InfoGibraltar, CC BY 2.0, via Wikimedia Commons) If you do have a background in probability theory, it doesn't hurt to remind yourself occasionally of its weirder aspects. Recreational puzzles like the daughters' problem are a good refresher.
If you don't have a background in probability theory, you need to realize you're liable to make errors of judgment with potentially serious business consequences. It's important to listen to technical advice. If you don't understand the advice, you have three choices: get other advisors, get someone who can translate, or hand the decision to someone who does understand.