The datasaurus: always visualize your data

The summary is not the whole picture

If you just use summary statistics to describe your data, you can miss the bigger picture, sometimes literally so. In this blog post, I'm going to show you how relying on summaries alone can lead you catastrophically astray and I'm going to tell you how you can avoid making career-damaging mistakes.

The datasaurus is why you need to visualize your data. Source: Alberto Cairo. Open source.

What are summary statistics?

Summary statistics are parameters like the mean, standard deviation, and correlation coefficient; they summarize the properties of the data and the relationship between variables. For example, if the correlation coefficient, r, is about 0.8 for two data sets x and y, we might think there's a relationship between them, but if it's about 0, we might think there isn't.

The use of summary statistics is widely taught, every textbook emphasizes them, and almost everyone uses them. But if you use summary statistics in isolation from other methods you might miss important relationships - you should always visualize your data as we'll see.

Anscombe's Quartet

Take a look at the four plots below. They're obviously quite different, but they all have the same summary statistics!

Here are the summary statistics data:

Property	Value
Mean of x	9
Sample variance of x : ${\displaystyle \sigma ^{2}}$	11
Mean of y	7.50
Sample variance of y : ${\displaystyle \sigma ^{2}}$	4.125
Correlation between x and y	0.816
Linear regression line	y = 3.00 + 0.500x
Coefficient of determination of the linear regression : ${\displaystyle R^{2}}$	0.67

These plots were developed in 1973 by the statistician Francis Anscombe to make exactly this point: you can't rely on summary statistics, you need to visualize your data. The graphical relationship between the x and y variables is different in each case and implies different things. By plotting the data out, we can see what the relationships are, but summary statistics hide what's going on.

The datasaurus

Let's zoom forward to 2016. The justly famous Alberto Cairo tweeted about Anscombe's quartet and illustrated the point with this cool set of summary statistics. He later expanded on his tweet in a short blog post.

Property	Value
n	142
mean	54.2633
x standard deviation	16.7651
y mean	47.8323
y standard deviation	26.9353
Pearson correlation	-0.0645

What might you conclude from these summary statistics? I might say, the correlation coefficient is close to zero so there's not much of a relationship between the x and the y variables. I might conclude there's no interesting relationship between the x and y variables - but I would be wrong.

The summary might not mean anything to you, but the visualization surely will. This is the datasaurus data set, the x and the y variables draw out a dinosaur.

The datasaurus dozen

Two researchers at Autodesk Research took things a stage further. They started with Alberto Cairo's datasaurus and created a dozen other charts with exactly the same summary statistics as the datasaurus. Here they all are.

The summary statistics look like noise, but the charts reveal the underlying relationships between the x and y variables. Some of these relationships are obviously fun, like the star, but there are others that imply more meaningful relationships.

If all this sounds a bit abstract, let's think about how this might manifest itself in business. Let's imagine you're an analyst working for a large company. You have data on sales by store size for Europe and you've been asked to analyze the data to gain insights. You're under time pressure, so you fire up a Python notebook and get some quick summary statistics. You get summary statistics that look like the ones I showed you above. So you conclude there's nothing interesting in the data, but you might be very wrong.

You should plot the data out and look at the chart. You might see something that looks like the slanting charts above, maybe something like this:

the individual diagonal lines might correspond to different European countries (different regulations, different planning rules, different competition, etc.). There could be a very significant relationship that you would have missed by relying on summary data.

(The Autodesk Research team have posted their work as a paper you can read here.)

Lessons learned

The lessons you should take away from all this are simple:

• summary statistics hide a lot
• there are many relationships between variables that will give summary statistics that look like noise
• always visualize your data!

Cheating charts: the axes of evil

As you might have guessed from the title, this post is all about how you can play around with chart axes to lie like truth. It's about being evil with axes.

In the Harry Potter books, the children are taught 'Defence Against the Dark Arts' not to teach them how to be evil, but rather to teach them how to defend against evil. I'm using the same approach here; this blog post is about defending yourself against being misleading or being misled.  I'm going to show you ways that people have used chart axes to obscure the truth. But we need to be careful with blame; sometimes, charts are unintentionally deceitful, the author miscommunicated rather than set out to misinform, and sometimes it's a matter of opinion. Read what I have to say and decide for yourself.

(2x2 matrix - an example of evil axes)

Zero axis

In most cases, charts should include zero so as not to mislead about the size of an effect. Let's take house prices in London as our example. UK inflation (CPI) was 1.8% for the twelve months from January 2019 to January 2020, over the same period, London house prices increased 2.8% - not a bad increase, but we can make it look much larger.

Let's start with an honest chart.

It clearly shows a small increase, but it would be hard to get a newspaper headline from it. Imagine you were a newspaper editor and you needed to squeeze a sensationalist story from the data. You need to make the difference appear much bigger, but still have a fig leaf of decency. How can you do it? The simplest way is excluding zero and zooming in.

Imagine that we coupled it with a headline like, 'London Property Market Booms' and had an article with examples of extremely expensive houses and some anecdotes of house buying. If you just glanced at the chart and read the story, you might think the market was growing explosively. This trick works even better if you make the axes text small, reduce their contrast with the background color, or even remove them altogether.

If you're trying to be honest, most of the time, you should include zeros to truly scale the effect and not mislead. But there are exceptions. Sometimes you do want to exclude zero as in the example below.

I have some data on human body temperature over the course of a day, taken from Wikipedia. Here's a chart including zero (as in 0 centigrade).

There really doesn't seem to be much variation does there? It looks like the human body temperature stays more or less constant during the day. In fact, the data looks just like noise. I could flatten the chart further by using degrees Kelvin or even showing a Fahrenheit scale starting from zero. 

When we zoom in and exclude zero, a clearer picture emerges.

Plainly, human body temperature does change during the day. Given the fact that a few degrees difference in body temperature can make the difference between someone who's fine and someone who's in medical danger, the second chart is a better and more honest and useful representation.

If you want to cheat and misrepresent, here's what you should do:

• If you want to exaggerate a small difference, don't include zero and zoom into your chart to expand the difference.
• If you want to suppress a difference, include zero and choose units that minimize the difference.

If you want to be honest:

• Include zero by default.
• Don't include zero when you're looking at small changes and the changes matter, in this case, exclude zero to focus on the change.

Extending the axis

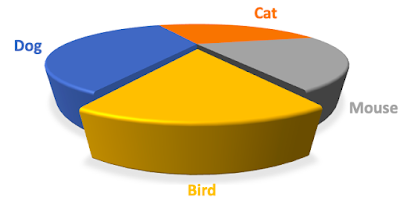
This is a really fun way to mislead people and it's something I've only seen recently. You can extend the perception of the axis to reduce the effect. Let's use the same election example I used in my blog post on pie (lie) charts. Imagine there are four parties standing in an election and you have a record of what percentage of the vote each candidate and party received. Here's an honest bar chart showing the results.

Plainly, the Bird party did very badly (15% of the vote). Now let's see if we can minimize the scale of their defeat by redrawing the chart in a deceitful way. Let's remove the x-axis, extend the y-axis labels, color and box the labels, and introduce some bar coloring.

It's still obviously a defeat, but we've made it look much smaller. If you take the time to look, it's obvious that something funky is going on here, but most people don't have time and don't look closely.

If you want to be honest, don't play around with axis labels and colors.

Unequal steps

If you want to imply things are getting worse, or better, when they're not, then a good option is to use unequal axis scaling. Most viewers expect that an axis will scale consistently, for example, an axis might be labeled 1, 2, 3, 4, 5, 6, 7, 8, 9, 10  and more sophisticated viewers might be very comfortable with log scales, for example, axis labels 1,10, 100, 1000. Almost no one can interpret what unequal scaling means, which makes it great for evil. To make your deception even better, use a line chart (which implies continuity) rather than a bar chart (which implies category).

Let's take an example that appeared in the media, US gas prices in 2012. The AAA produces a daily set of gas price data. This has today's price, yesterday's price, last week's price, last month's price, and last year's price. It's not the greatest presentation of data and it's hard to pick out trends, but at least the data exists - and more importantly, they don't chart it. In 2012, a US media outlet (who shall remain nameless) took the data and ran a story on gas price increases under Obama. Here's my version of their chart.

At a quick glance, it looks like there was a massive increase. But was there? The periods on the x-axis aren't equal and they've used a line to indicate a continuous variable. The AAA data quotes last month's number, but that isn't shown here, why? The y axis starts at $2.80 which is an odd choice, more rational choices might have been $3.00 or $0. If you take the time to look at the chart, it's really hard to draw any conclusions, but most people don't have the time and will just conclude 'gas prices up under Obama'.

If you really want to mislead, use unequal scaling and a line chart.

Scale inversion

If you really, really want to mislead, choose a scale inversion. 

I'm going to show you one of the most controversial charts of the last ten years. The author has vigorously defended their work, and after reading their comments, I understand that they had no intention to deceive. Because I don't wish to make the author's life more difficult, I'm not going to name them or give you their employer's name.

The chart below shows homicides in Florida and what happened when the 'Stand Your Ground' Law was enacted. Before reading on, how would you interpret the chart?

Almost everyone I've spoken to interprets the chart as implying that homicides went down. But look at the y axis. It's inverted. Here's how the plot would look if the author had chosen normal scaling.

This conveys a hugely different message.

The author wasn't trying to mislead here, rather they were trying to use art to make a more emotionally informative representation of the data. You can judge for yourself whether they succeeded or not. This raises the more general topic of who is visualizing data and how it's done. 

In the last few years, there's been a tremendous rise in the use of infographics for all kinds of topics. These tend to be more poster art than information sharing, which leads us to a problem. In the information world, a large number of informal practices have grown up around how to display data in a truthful way. Infographics are sometimes created by people familiar with these practices, but sometimes not. When designers start using artist interpretation to make data more impactful, we can get distortions and unintentionally misleading people. Personally, I think infographics are little more than visual fluff.

Getting back to where I started in this section, scale inversion is a wonderful way of reversing the evidence.

Log plots

This isn't so much deceit as obfuscation or confusion.  

A logarithmic scale is one that varies logarithmically, so instead of an axis increasing like 1,2,3,4,5, it increases like 1, 10, 100, 1000, 10000. Logarithmic scales are used when data varies by orders of magnitude. 

Unfortunately, many viewers aren't familiar with the idea and it can be hard to interpret, a good example being the recent coronavirus chart in a New York Times article. Here's the chart:

(Imaged credit: New York Times, copyright New York Times)

The logarithmic axis is the y axis. What conclusions would you draw about the coronavirus from this chart? I've used log plots for years and I struggled to understand what this chart means. 

2x2 charts

2x2 charts are a special case of confusion with axis. Unfortunately, they're beloved of MBA courses and books on management and marketing. Let's take the classic BCG product matrix as an example. In the 1960s, the consulting company BCG came up with a way for companies to view their product portfolio and make more rational product investment decisions. They recommended plotting market share on the x-axis, growth on the y axis, and dividing the plot into four quadrants, each with a name, you can read more about it here. Here's a representation of their matrix.

Note that although the axes are marked, there's no scale and it's not clear where the quadrant lines are drawn. In practice, companies using this methodology may well draw scales, but in almost all cases you find on the internet, there are no scales.

The BCG matrix is just one of a large number of 2x2 matrices you can find out there. Very few of them have any kind of scale, so it's very hard to understand and interpret what they mean in practice. Bear in mind that they often imply quite different management choices for different chart quadrants, but who's in what quadrant may depend on exactly where the quadrant boundaries are drawn, and that's almost never made clear. It's really tempting to say that you need to employ consultants to tell you what they mean and to interpret the charts for you.

I'm not a fan of 2x2 matrices because I find that they confuse rather than enlighten, but if you want to produce a chart that looks pretty and requires you to interpret it for your management, a 2x2 matrix might well be the place to go.

You can fool all the people some of the time and some of the people all the time

If you know what you're looking for, you can see through deceit or malpractice with some effort. But if you're in a hurry, not paying attention, or a chart is flashed on the screen for a short period of time, a chart with evil axes will probably slip by your defenses against the dark arts.

In many ways, playing around with chart axes is one of the easiest ways to mislead people. I've shown you how people have been evil with axes in the hope that you'll be truthful and honest in your own visualizations.

I'd love to hear what you think about the 'axes of evil'. Have you come across other axis manipulations that I haven't included here?

Pie charts are lie charts

There are lots of chart types, but if you want to lie or mislead people, the best chart to use is the pie chart. I’m going to show you how to distort reality with pie charts, not so you can be a liar, but so you know never to use pie charts and to choose more honest visualizations.

Let's start with the one positive thing I know about pie charts: they're called camembert charts in France and cake charts in Germany. On balance, I prefer the French term, but we're probably stuck with the English term. Unlike camembert, pie charts often leave a bad taste in my mouth and I'll show you why.

(Camembert cheese - image credit: Coyau, Wikipedia - license : Creative Commons)

Take a look at the pie chart below. Can you put the six slices in order from largest to smallest? What percentages do you think the slices represent?

Here’s how I’ve misled you:

• Offset the slices from the 12 o’clock position to make size comparison harder. I've robbed you of the convenient 'clock face' frame of reference.
• Not put the slices in order (largest to smallest). Humans are bad at judging the relative sizes of areas and by playing with the order, I'm making it even harder.
• Not labeled the slices. This ought to be standard practice, but shockingly often isn't.

The actual percentages are:

Gray	20.9
Green	17.5
Light blue	16.8
Dark blue	16.1
Yellow	15.4
Orange	13.3

How close were you? How good was my attempt to deceive you?

Let’s use a bar chart to represent the same data.

Simple, clear, unambiguous.

I've read guidance that suggests you should only use a pie chart if you're showing two quantities that are obviously unequal. This gives the so-called pac-man pie charts. Even here, I think there are better representations, and our old-friend the bar chart would work better (albeit less interestingly).

Now let’s look at the king of deceptive practices, the 3d pie chart. This one is great because you can thoroughly mislead while still claiming to be honest. I’m going to work through a short deceptive example.

Let’s imagine there are four political parties standing in an election. The percentage results are below.

Dog	36
Cat	28
Mouse	21
Bird	15

You work for Bird, which unfortunately got the lowest share of the vote. Your job is to deceive the electorate into thinking Bird did much better than they did.

You can obscure the result by showing it as a pie chart without number labels. You can even mute the opposition colors to fool the eye. But you can go one better. You can create a 3d pie chart with shifted perspective and 'point explosion' using the data I gave above like so.

Here's what I did to create the chart:

• Took the data above as my starting point and created a pie chart.
• Rotated the chart so my slice was at the bottom.
• Made the pie chart 3d.
• Changed the perspective to emphasize my party.
• Used 'point explosion' to pull my slice out of the main body of the chart to emphasize it.
• Used shading.

This now makes it look like Bird was a serious contender in the election. The fraction of the chart area taken up with the Bird party’s color is completely disproportionate to their voter share. But you can claim honesty because the slice is still the correct proportion if the chart was viewed from above. If challenged, you can turn it into a technical/academic debate about data visualization that will turn off most people and make your opponents sound like they’re nit-picking.

You don’t have to go this far to mislead with a pie chart. All you have to do is increase the cognitive burden to interpret a chart. Some, maybe even all, of your audience might not spot what you’re trying to hide because they’re in a hurry. You can mislead some of your audience all of the time.

I want to be clear, I'm telling you about these deceptive practices so you can avoid them. There are good reasons why honest analysts don’t use pie charts. In fact, I would go one stage further; if you see a pie chart, be on your guard against dishonesty. As one of my colleagues used to say, ‘friends don’t let friends use pie charts’.